Hidden Math: The Numbers That Make LEGO Work
/What math is hidden in your favorite LEGO sets, how can you recognize it, and how does it magically make LEGO geometry work so perfectly? Best of BrickNerd - Article originally published June 10, 2022.
To help answer those questions, we are pleased to feature a guest article from Deep Shen discussing the hidden math in LEGO. Deep’s amazing portfolio of work can be found at Towering Brick Creations, on his Flickr page and on Instagram.
Hidden Math
I am sure I speak for all AFOLs when I say that building official LEGO sets can be quite an enjoyable experience. It is always exciting to crack open the box, find all the numbered bags, and start putting the model together based on the instructions. But every so often there is a technique we come across that confounds us and leaves us wondering, “How does that even work?”
It is a safe bet to assume that the answer lies in the hidden math lurking behind all things LEGO. You probably recall the simple math that comes into play with sideways building or SNOT. Instead of rehashing it here, let me refer you to this excellent article on SNOT. But there are other techniques that are a little more advanced that place LEGO elements outside the confines of the regular square grid to create angled walls or round shapes. Here the math can get a tad more - shall we say, nerdy? Not to worry, you won't find anything in this article that you haven't already come across in high school math.
If math is such an integral part of LEGO, does it mean that LEGO designers need to always have a calculator or a whiteboard handy to work out the numbers? Not really. The beauty of the LEGO system is that there are literally infinite different ways of putting the pieces together. If you spend enough time playing with LEGO (you would expect the designers at LEGO to be doing just that), you are bound to stumble upon new and interesting techniques without always being cognizant of the underlying math.
Sometimes I wonder if a brilliant connection in a new set is planned out by the numbers or just sheer happenstance in the design process. No matter the reason, being a nerd myself, it is quite fascinating for me to reverse engineer some of the clever techniques used in official sets to try to uncover the math that makes them work.
Angled Walls Using Pythagorean Triples
Let’s start with the latest modular building set from LEGO – the Boutique Hotel 10297 which was released on January 1, 2022. The first thing that draws your attention to this modular building is its unusual triangular shape. LEGO as we know is based on a regular square grid of stud locations and so how did they pull off this shape and can we figure out the math behind it?
If you read my post on angled walls, you will see that the trick to placing LEGO pieces at any angle other than 0 or 90 degrees relative to the LEGO grid is by ensuring that the studs at the two ends of the brick or plate line up with studs on the LEGO grid. This only works when the resulting right-angled triangle satisfies the Pythagorean theorem (a²+b²=c²). The smallest Pythagorean triple (set of numbers that satisfies the theorem) is (3,4,5) and that is the one the Boutique Hotel uses. But it uses the triple in a way that is not immediately apparent. In fact, if you look at the angled walls in this build, you can count not one but six separate (3,4,5) triangles including two (4 and 6) that even intersect each other.
Given that the hypotenuses (longest sides) of triangles 1-4 are in a straight line connected together using long plates, we don’t even need to connect the outer ends of triangles 1 and 4. The hypotenuses of triangles 5 and 6 are at right angles to the line connecting the hypotenuses of triangles 1-4.
The Mirrored Hypotenuse Technique
Even more interesting is the fact that the floor sections separating the three levels of the building as well as the roof section are built using regular plates and wedge plates, and somehow, their angled sides line up perfectly with the angled walls of the building. Coincidence? I think not. We will need to get into some basic trigonometry to explain this.
In a right-angled triangle for either of the smaller angles, the ratio of the length of the side opposite the angle to the side adjacent to it is called the tangent. This ratio is fixed for a given angle regardless of the size of the triangle. If we already know the ratio, we can figure out the angle using the inverse of the tangent function or arctan (available in most scientific calculators). In a (3,4,5) triangle, the tangent of the smallest angle is 3/4 = 0.75 and the arctan of that is 36.8 degrees.
If you look at one of the floor sections or the roof section of the Boutique Hotel, you will see that they use two mirrored 6×3 wedge plates to create the angled side. Each wedge plate has a right triangle with a tangent of 2/6 = 0.333 and the arctan of that is 18.4 degrees. So it makes sense that two of these wedge plates would give us a combined angle of 36.8 degrees matching what we have on the angled wall.
We can confirm this using the formula to calculate the tangent of twice a given angle.
Plugging in the numbers, we see that the tangent of twice the angle created by the wedge plate is (2 x 1/3) / (1 – 1/9) = 2/3 x 9/8 = 3/4 which matches the tangent of the angle created by the (3,4,5) Pythagorean triple. Pretty neat, eh?
The way the wedge plates are used here is a common application of the "mirrored hypotenuse" technique also covered in my post on angled walls. This gets around the fact that for an arbitrary right triangle, the length of the hypotenuse is not always a whole number. The hypotenuse for the triangle created by the 6x3 wedge plate is √(6² + 2²) = 6.32 studs. Even though we cannot place a LEGO element along the hypotenuse, we can create an angled wall by mirroring the right triangle along the hypotenuse and placing LEGO elements along the other two sides of the second triangle. The two triangles have to be held together using hinge plates and this is exactly what is done in the Boutique Hotel set.
Angled Walls Using Turntables
Angled walls can also be built using turntables, and you can see this in multiple official sets. An example is the Spring Lantern Festival set (80107) where 4×4 turntables are used to attach an arched footbridge at an angle over a koi pond.
A LEGO turntable consists of a base (2×2 or 4×4) which can be attached like a normal plate and a top that can swivel freely by a full 360 degrees. The 2×2 base requires a matching top element while the 4×4 base can accommodate a variety of compatible elements including a 4×4 round plate.
Even when we are using turntables to create an angled wall (or a structure attached at an angle, as in this example), we are essentially creating a right-angled triangle that satisfies the Pythagorean Theorem. The sides of this triangle intersect at the axes of rotation on the turntables (the center points of top plates). The Pythagorean Triple used in this case is (6,8,10).
Angled Walls Using "Near Triples"
As we have seen, we don’t have a lot of options to choose from if we just limit ourselves to Pythagorean Triples. Most applications of the Pythagorean Theorem use the smallest and most common triple (3,4,5) as in the Boutique Hotel set or a multiple like (6,8,10) used in the Spring Lantern Festival set.
However in certain situations, it is possible to fudge the math a bit and get away with a triple (set of three numbers) that is not a Pythagorean triple strictly speaking but is close enough for practical purposes. I like to call these “near triples”.
When we create angled walls using “near triples”, it is always a good idea to use elements like hinges that naturally have a little bit of wiggle room. This minimizes the strain that you are putting on the LEGO elements when you make the connections for the angled section.
I have used “near triples” like (5,5,7) and (7,7,10) often in my builds and some of these have the added advantage of allowing us to create walls at 45-degree angles (which is not possible with Pythagorean Triples). I wasn’t aware of any official sets that used “near triples” until I looked through the instructions for the Corner Garage 10264 modular set that LEGO released in early 2019.
One notable aspect of this modular is that a large part of the front façade of the garage is built at a 45-degree angle. There is also an awning above a gas station island that is attached perpendicular to that façade (and ends up being at a 45-degree angle relative to the base).
If we dig into the instructions for this set, we see that the angled section is built on a 2×16 plate that is attached at a 45-degree angle using 1×2 rounded plates. The total length of the angled section is 17 studs measured between the studs at the two connection points.
If we think of this as the hypotenuse of a right triangle, the other two sides would each be 12 studs long (if you picture horizontal and vertical lines drawn along the LEGO grid from the studs at the two connection points, they would intersect at a stud that is 12 studs away in each direction).
Now, (12,12,17) is not a Pythagorean triple strictly speaking. But the length of the hypotenuse in a right triangle where the other two sides are 12 is √(12² + 12²) = 16.97 which is close enough to 17. The 1×2 rounded plates act like hinges and provide a firm connection while allowing a little bit of wiggle room.
“Near triples” also come into play in the way the awning is attached at a 45-degree angle (relative to the baseplate). But it is a little less obvious how the math works here. Taking a closer look, we see that the awning is 16×10 studs wide with rounded corners. It is attached to the angled wall of the garage using a hinge assembly consisting of a 1×3 tile with one finger on top (attached to the angled wall) and a 1×2 brick with two fingers (which is incorporated into the awning itself).
The awning is supported by two vertical posts that are created using technic axles and axle connectors. These posts connect the awning to the gas station island but the island itself is connected to the base in just one spot. There is a good reason for that.
The gas station island has two 4×4 round plates that are 6 studs apart (center to center) but there is no way to connect both these at a 45-degree angle given that there are no “near triples” with 6 as the biggest number. So the designers chose to connect one side of the gas station island to a 2×2 tile with a hole (this attaches to the bottom of the 4×4 round plate to form a turntable) and leave the other side unconnected (it simply rests on the 2×2 black turntable base).
We can look at the side that actually has a connection and try to figure out the math that is involved. The connection point is exactly 13.5 studs from the line connecting the ends of the angled façade. This can be broken up into two “near triples”. First, we start with the right triangle representing the original “near triple” (12,12,17).
If we draw a line from the vertex (corner) opposite the longest side (or hypotenuse) so it intersects the hypotenuse at a right angle, we would get two identical right triangles with dimensions (8.5,8.5,12). This is also a “near triple” so we can think of 8.5 out of 13.5 to be one of the legs (shorter sides) of this smaller right triangle. The remaining 5 is the hypotenuse (longest side) of another “near triple” (3.5,3.5,5). Pretty cool, right!?
Round Shapes Using Turntables
Turntables can also be used in other interesting ways like creating round shapes. In April 2022, LEGO announced two new additions to their Botanical Collection line. I will be talking about one of them (10311 Orchid) in this article. What kind of math could possibly be involved in a set with flowers anyway? Extra credit points if you correctly guessed that I am talking about the vase, of course! At first glance, it almost seems miraculous how the fluted vase is put together with its perfectly round shape and double slopes attached on the outside with nary a gap to be found between them.
The vase was the first thing that caught my eye when I saw the announcement for the Orchid set (although I have to admit that the rest of it is pretty neat too). It is not always easy to create round shapes using LEGO (I have covered a few different ways in my previous BrickNerd article). The designer of the Orchid set (Mike Psiaki, who is also responsible for the Titanic and Apollo Saturn V sets among others) has come up with a very clever way that relies on the mathematical properties of the 8×8 round plate which we will now examine.
The 8×8 round plate is a relatively new addition to the LEGO catalog joining its smaller siblings (such as the 4×4 and 6×6 round plates). But one thing that is neat about the 8×8 round plate is that all the studs on its periphery are located at about the same distance from the edge of the plate and this includes the studs along the diagonals. This is not true for the 6×6 round plate where the studs along the diagonals are inset a little bit from the edge of the plate.
To understand why, let us consider the diagonal distance between two studs which is √2 times a stud dimension (0.8 cm) which equals 1.13 cm. On the 6×6 round plate, the distance between the outermost studs along the diagonals is 3 x 1.13 = 3.39 cm = 4.24 studs whereas on a 8×8 round plate it is 5 x 1.13 = 5.65 cm = 7.06 studs which is very close to the 7 stud separation between the outermost studs along the horizontal and vertical axes.
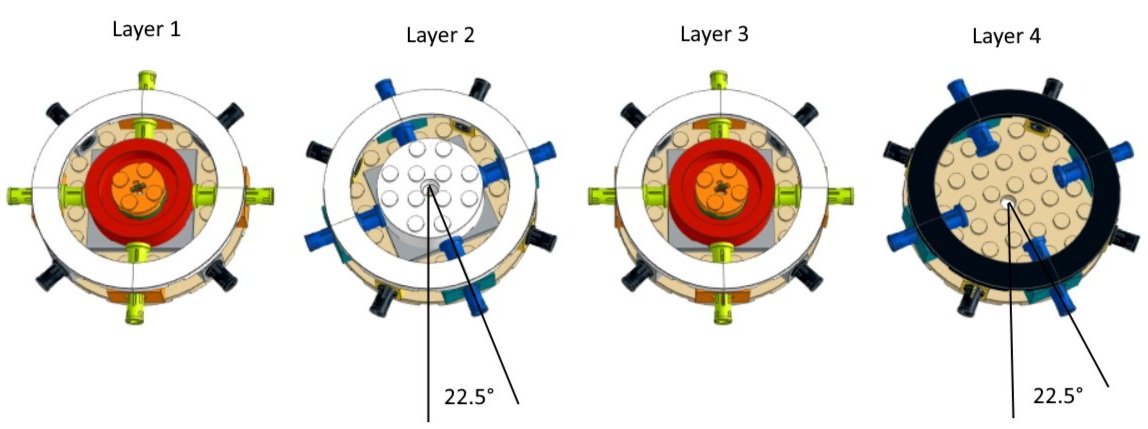
What this allows us to do is place Technic bricks along the outer edge of the 8×8 round plate with technic pins sticking out by about the same amount on all sides. Of course, the 1×1 Technic bricks along the diagonals need to be rotated by 45-degree angles. The 8×8 round plate with eight Technic pins sticking out is just one of four layers that are stacked and rotated using turntables to make up the core of the vase.
The angle of rotation of the even layers (layers 2, 4) is half of 45 degrees or 22.5 degrees. This places the eight Technic pin locations on the even layers exactly halfway between the eight Technic pin locations on the odd layers. When all four layers are stacked we have a total of 16 columns of technic pins spaced evenly along the circumference of the core.
16 Technic 1×7 liftarm pieces can be attached to these technic pins allowing us to then attach the double slope pieces needed to create the fluted appearance. Notice that with the 4×4 macaroni tiles added on the top, the height of each layer is 5 plates and this ensures the correct vertical spacing between the Technic pins when the layers are stacked (5 plates as we know from the basic SNOT equation is equivalent to 2 studs).
Why do we even need the liftarm pieces? Why not use SNOT bricks instead of the Technic bricks and attach the double slope pieces to them directly? We again need some math to help explain this. The diameter of the 8×8 round plate is 8 studs or 20 plates. With the liftarm pieces (which are 1 stud thick) attached on both sides, the total diameter becomes 20+2.5+2.5=25 plates.
The circumference of the core is now π x 25 = 78.5 plates. Now divide that by 16 and you get 4.9 plates which is very close to the 5 plate (2 stud) width of each double slope piece. Now we see how the liftarm pieces help make the inner core just large enough to attach the double slope pieces all around with almost no gaps showing between them.
Conclusion
Hopefully this article succeeds in piquing your interest about the math that is hiding behind everything that you build with LEGO. As long as you don't mind getting your hands dirty with a little math, there are a lot of cool techniques you can pick up from official LEGO sets (that could even come in handy when you design your own MOCs). Speaking of MOCs, I hope to cover at least a few of them in a follow-up article. In the meantime, if there are any techniques used in official LEGO sets that still have you scratching your head, please feel free to post a comment here. Happy building!
Have you noticed any brilliant math used in any of your favorite LEGO sets? Let us know in the comments below!
Do you want to help BrickNerd continue publishing articles like this one? Become a top patron like Charlie Stephens, Marc & Liz Puleo, Paige Mueller, Rob Klingberg from Brickstuff, John & Joshua Hanlon from Beyond the Brick, Megan Lum, Andy Price, John A., Lukas Kurth from StoneWars, and Wayne Tyler to show your support, get early access, exclusive swag and more.